密码学
术语
(1)消息(Message):消息是指用语言、文字、数字、符号、图像、声音或其组合等方式记载或传递的有意义的内容。在密码学里,消息也称为信息 。
(2)明文(Plaintext):未经过任何伪装或隐藏技术处理的消息称为明文。
(3)加密(Encryption):利用某些方法或技术对明文进行伪装或隐藏的过程称为加密。
(4)密文(Cipher Text):被加密的消息称为密文。
(5)解密(Decryption):将密文恢复成原明文的过程或操作称为解密,解密也可称为脱密。
(6)加密算法(Encryption Algorithm):将明文消息加密成密文所采用的一组规则或数学函数。
(7)解密算法(Decryption Algorithm ):将密文消息解密成明文所采用的一组规则或数学函数。
(8)密钥(Key):进行加密或解密操作所需要的秘密参数或关键信息 。在密码系统中,密钥分为私钥与公钥两种。私钥指必须保密的密钥,公钥指可以向外界公开的密钥。
(9)密码系统 (Cryptosystem ):一个密码体制或密码系统是指由明文空间、密文空间、密钥空间、加密算法以及解密算法 组成的一个多元素集合体。
分类
加解密
对称加密(Sysmmetric Cryptography)(使用相同密钥)
非对称加密(Public-Key Cryptography,Asymmetric Cryptography)(使用不同密钥)
这两者的区别是是否使用了相同的密钥,对称与非对称加密是可以通过密钥解出明文。因为明文不定,密文必定是不定长。
单向散列
单向散列可以是定长的,结合密码学的加解密技术和单向散列技术,又有了用于防止篡改的消息认证码技术,防止伪装的数字签名技术以及认证证书。
技术支持
| 攻击方式 | 特征 | 对应技术 |
|---|---|---|
| 窃听 | 机密性 | 对称、非对称加密 |
| 篡改 | 完整性 | 单向散列、消息认证码、数字签名 |
| 伪装 | 身份认证 | 消息认证、数字签名 |
| 否认 | 不可否认 | 数字签名 |
加密简介
对称加密
由于其速度快(根据相同密钥进行加解密),对称性加密通常在消息发送方需要加密大量数据时使用。对称性加密也称为密钥加密。
安全的重点:密钥管理的安全性、加密算法的复杂性
分组密码(归类对称加密):每次只能处理特定长度的一块(block)数据的一类加解密算法。分组加密的典型算法:DES、3DES、AES
分组密码的两个原则:
- 扰乱原则:加解密变换过程中将明文、密钥以及密文之间的关系尽可能地复杂化,即将明文、密钥以及密文之间的依赖关系复杂化,使密码分析者尽可能无法利用这种依赖性。
- 扩散原则:将算法设计成明文每一比特的变化尽可能多地影响到输出密文序列的变化,以便隐蔽明文的统计特性。即明文和密钥中任何一比特值发生变化,都会在某种程度上影响到密文值的变化,以防止将明文或密钥分解成若干孤立的小部分,然后被各个击破。
DES算法
DES的名称为:数据加密标准(Data Encryption Standard),是一种使用密钥加密的块算法
注意:
1.DES加密需要进行16轮的函数循环迭代。
2.密钥位64位,但是只有56位为有效位(其中8位为奇偶校验)。
全部操作步骤
- 输入64bit的明文进行IP置换,分成左右两个分支各为32bit, 左边:32bitL
0,右边:32bitR0- 右分支:L
1= R0,左分支:引入48bit 的密钥,R1=L0异或 f(R0,K1)- 相同的操作进行16次的运算循环,算出相应的,R
1–R16,L0–L16- 最后在进行IP的逆序置换,将左右两个分支再次合并为64bit密文
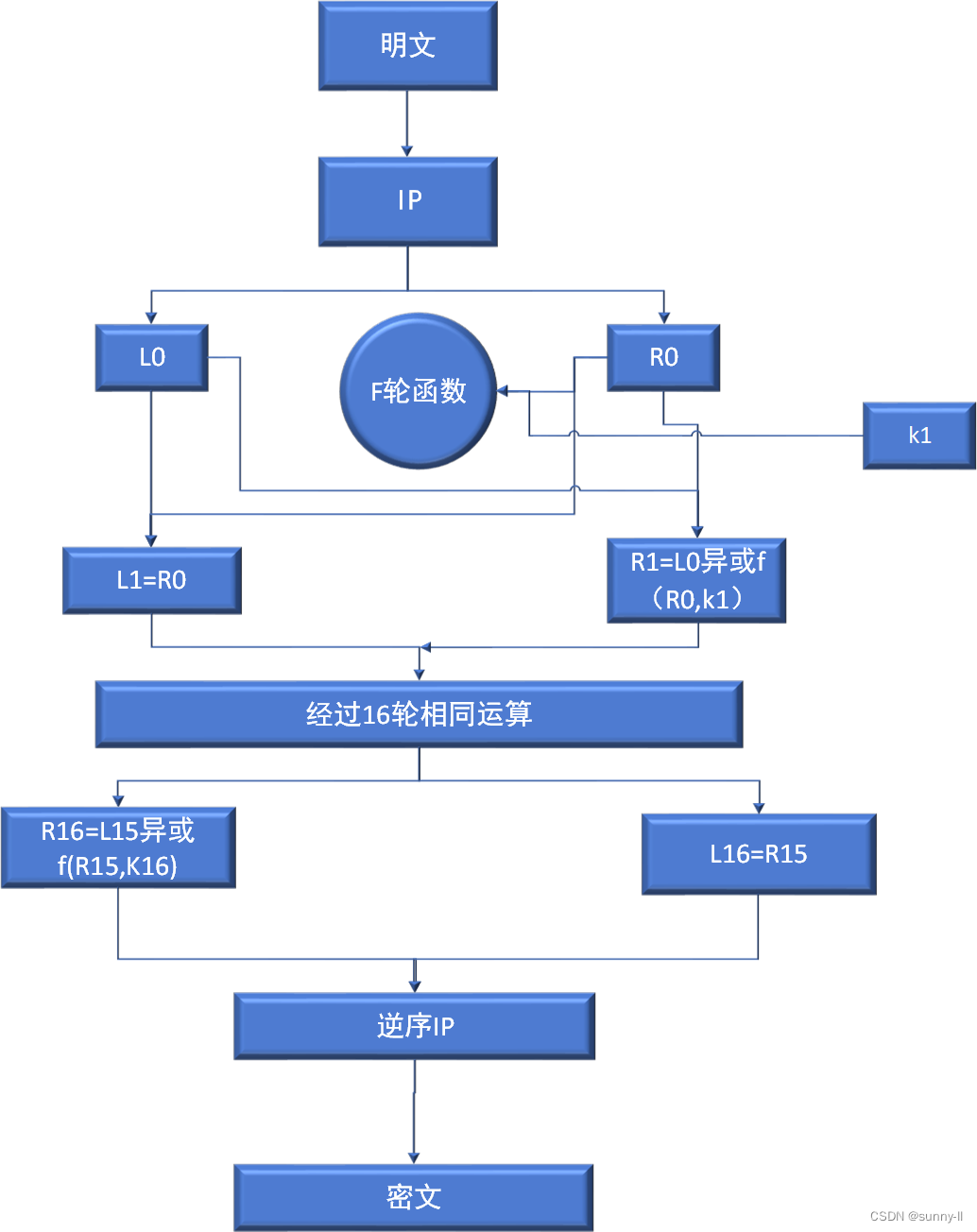
一次操作步骤
(1)明文IP置换分组
按固定表置换IP,后分组:Ln=32bit Rn=32bit
(2)F函数操作
Rn的E盒拓展、s盒替代、P盒置换
(3)密钥的形成
PC-1置换、分组、循环移位、PC-2置换
(4)Rn=L
n-1异或 f(Rn-1,K1)*第十六轮后需要进行逆序IP
(1)明文IP置换分组
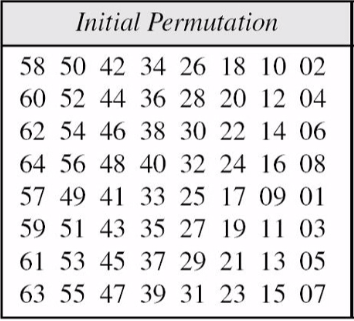
将IP进行上面的置换,再将置换后的IP分成L0=32bit,R0=32bit
第一个位置代表原来IP矩阵中58位置的置换到1位置(该表是固定且有规律的)
(2)F函数操作
- Rn的E拓展
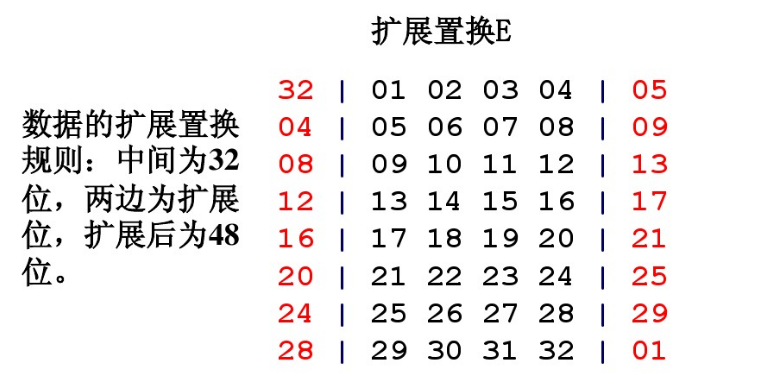
按上面的E盒对32位的Rn拓展成48位Rn
s盒替代
将E盒输出的48位替换压缩为32位
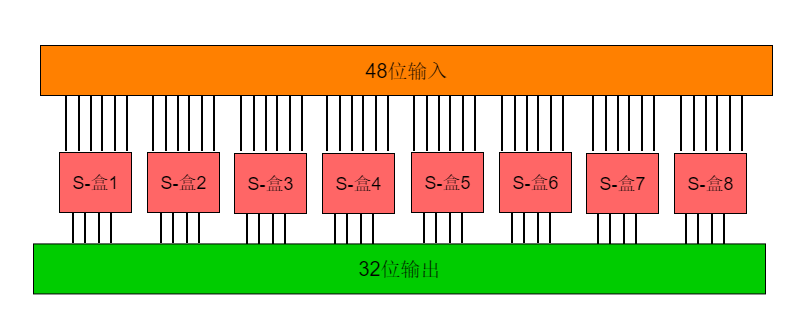
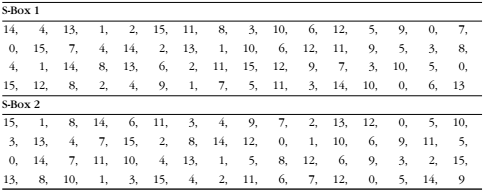
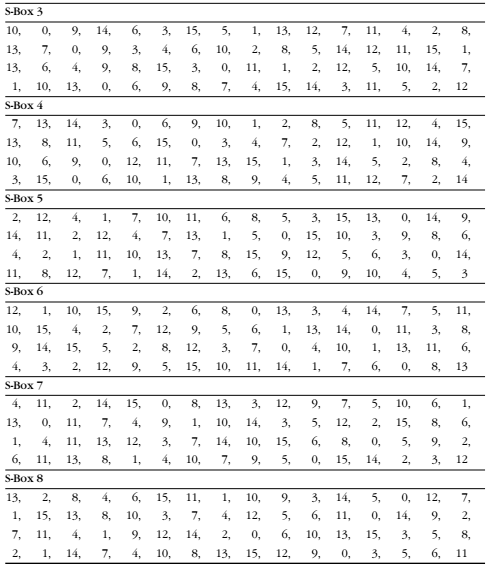
将Rn拓展后再与K异或后的48bit分成8个6bit,对应8个s盒。然后转化为2进制计算:Sn(h1….h6)对应Si表中的(h1,h6)行,(h2,h3,h4,h5)列,即Sn(h1….h6) = Si((h1,h6),(h2,h3,h4,h5))。**[行和列的开头为0]**
例如:111001 为对应S
1盒的6bit即行为:(11)
2= 3即列为:(1100)
2= 12前6位bit替换成新的4bit:S
i(3,12) = 10 = (1010)2
P盒置换
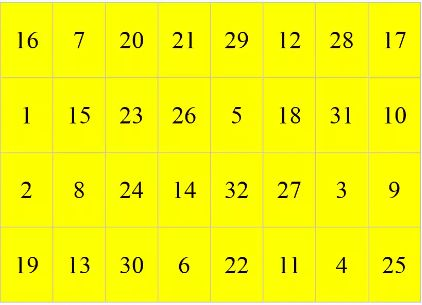
将S盒替换后的32bit再按P盒置换,规则如IP置换相同
(3)密钥的形成
PC-1置换
按pc-1表进行置换
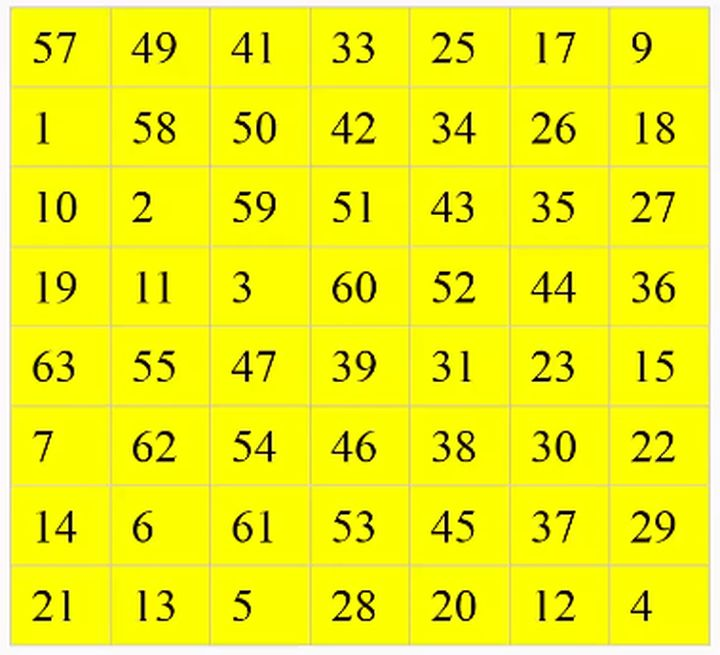
置换后发现64位密钥变成了56位(除去8位奇偶检验位)
- 分组
将PC-1置换后的56位分组,Cn=前26位,Dn=后26位
- 循环移位

按上面的轮数使得Cn和Dn向左移动位数
- PC-2置换
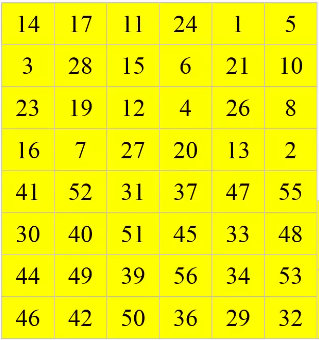
将循环移位后的内容按PC-2盒置换得到子密钥kn
(4)Rn=Ln-1 异或 f(Rn-1,K1)
双重DES
使用两个不同的密钥进行两次加密,期待密钥长度扩展为112bit,增加加密的安全性
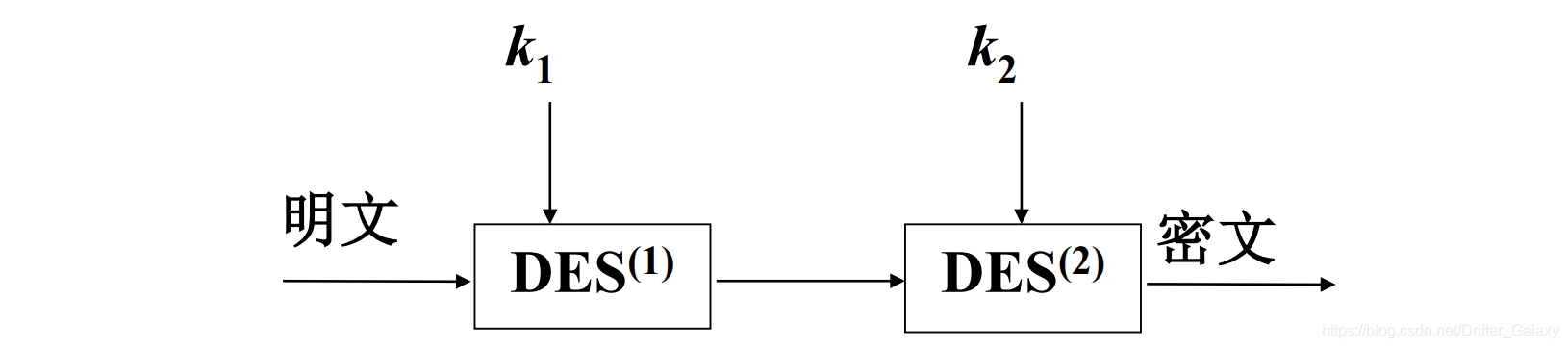
加密:C=Ek2[Ek1[P]]
解密:P=Dk1[Dk2[C]]
注意:该加密算法存在中间相遇攻击
k1和k2的可能性为1/2^56,使用明文对k1的所有可能密钥进行加密获得x1,使用密文对k2的所有可能密钥进行解密获得x2,对比x1和x2,如果存在一个中间相同的值则可以求出正确的k1和k2。
即:D
k2[C] = X = Ek1[P]时候k1和k2是正确的
破译复杂度:2^57量级
三重DES
使用三个密钥对信息进行加密解密操作,当k1=k3的时候称为双密钥三重DES
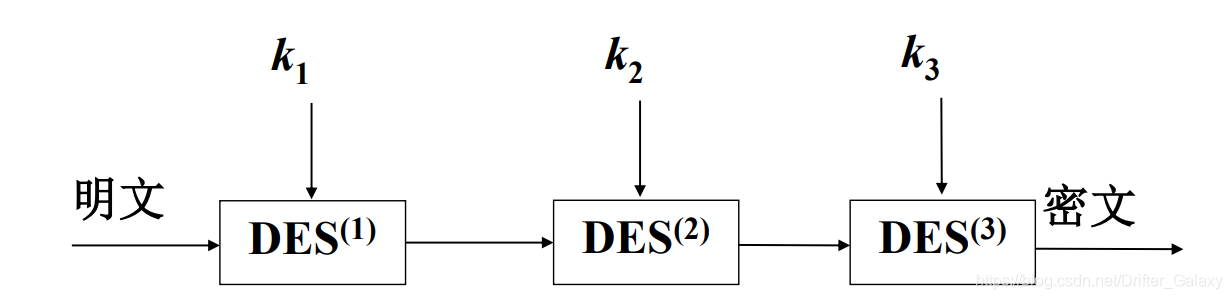
加密:C=Ek1[Dk2[Ek3[P]]]
解密:P=Dk3[Dk2[DK1[C]]]
破译复杂度10^52量级
AES算法
高级加密标准(Advanced Encryption Standard)是区块加密标准。
基本结构
| AES | 密钥长度(32位比特字) | 分组长度(32位比特字) | 加密轮数 |
|---|---|---|---|
| AES-128 | 4 | 4 | 10 |
| AES-192 | 6 | 4 | 12 |
| AES-256 | 8 | 4 | 14 |
AES的处理单位是字节,128位的输入明文分组P和输入密钥K都被分成16个字节,分别记为P = P0 P1 … P15 和 K = K0K1 … K15。
明文分组用字节为单位的正方形矩阵描述,称为状态矩阵(按列排序),如下:
| S |
S |
S |
S |
|---|---|---|---|
| S |
S |
S |
S |
| S |
S |
S |
S |
| S |
S |
S |
S |
128位密钥也是用字节为单位的矩阵表示,矩阵的每一列被称为1个32位比特字。通过密钥编排函数该密钥矩阵被扩展成一个44个字组成的序列W[0],W[1], … ,W[43],该序列的前4个元素W[0],W[1],W[2],W[3]是原始密钥
| K |
K |
K |
K |
|---|---|---|---|
| K |
K |
K |
K |
| K |
K |
K |
K |
| K |
K |
K |
K |
W[0]=K0K1K2K3
W[1]=K4K5K6K7
….
全部操作步骤
- 密钥拓展
- 轮密钥加
- 字节替换
- 行移位
- 列混淆(加密最后一轮没有该步骤)
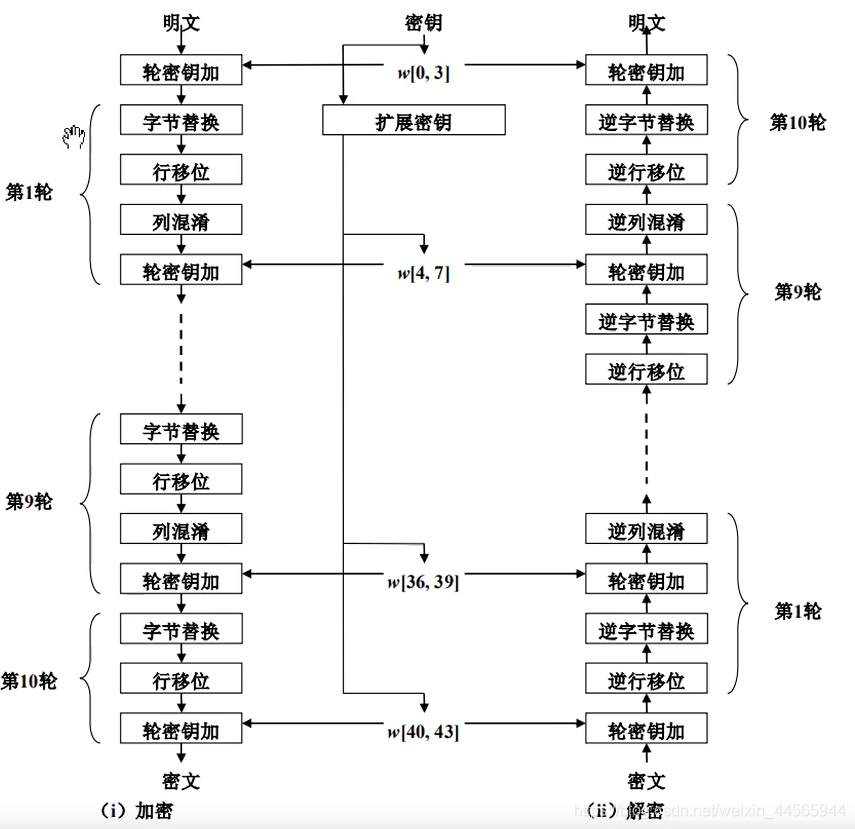
(1)密钥拓展
密钥拓展将一个128位的密钥扩展10次变成11个128位的密钥来用于接下来的轮密钥加操作
拓展步骤:
当i不为4的倍数的时候:W[i] = W[i-4] 异或 W[i-1]
当i为4的倍数的时候:W[i] = W[i-4] 异或 T(W[i-1])
T函数:
- 字循环:将W[i-1]向左移动(即在矩阵中的列向上移动一个字节)
- 字节替换:使用给定的S盒进行替换(第一个字节为行,第二个字节为列)
- 轮常量异或:将字节替换的结果与对应轮常量进行异或,i代表轮数
i 1 2 3 4 5 6 7 8 9 10 11 RC[i] 0x01 0x02 0x04 0x08 0x10 0x20 0x40 0x80 0x1B 0x36 0x6c 注意溢出操作:RC[i] = RC[i] 异或 0x1B
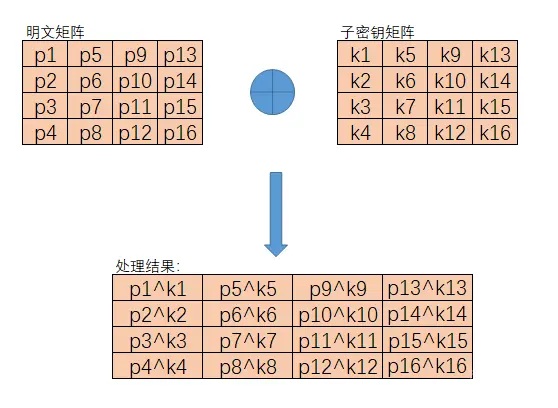
(2)轮密钥加(第一轮是与原始密钥矩阵)
明文矩阵和当前轮次的子密钥矩阵进行异或运算
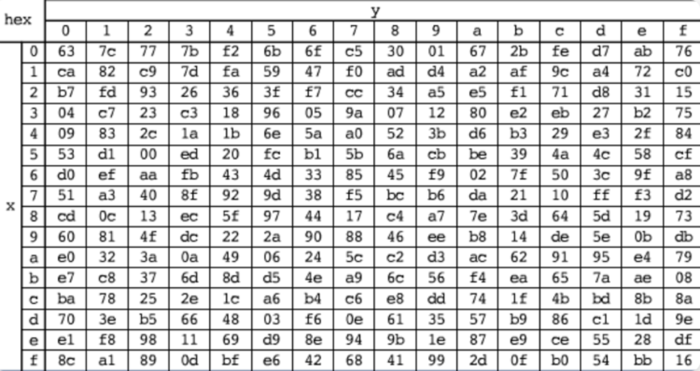
(3)字节替换
参考提供的S盒对明文完成一个字节到另外一个字节的映射。其中第一个字节为行,第二个字节为列。
例如 :0x01映射为0x7c
(4)行移位
第一行不变
第二行左移1位
第三行左移2位
第三行左移3位

(5)列混淆
列混淆操作是 AES 算法中主要的扩散元素,对状态矩阵(明文分组)中的每列进行独立操作,它混淆了输入矩阵的每一列,使输入的每个字节都会影响到 4 个输出字节。【使用定义的固定矩阵进行列混淆】
(1)计算值为固定矩阵的行 * 状态矩阵的列为对应的位置值

其中b0 = 02 * a0 异或 03 * a1 异或 01 * a2 异或 01 *a3
下面是一些相关知识
AES固定的不可约多项式:m(x) = x^8 + x^4 + x^3 + x + 1
十六进制{57}对应多项式:x^6 + x^4 + x^2+ x + 1
加法计算步骤:
例子:{57} + {83} = {D4}
- 转化
0x57 的二进制: (0101 0111)
2多项式: (x^6 + x^4 + x^2+ x + 1)
0x83 的二进制: (1000 0011)
2多项式: (x^7 + x + 1)
- 异或操作
多项式异或:(x^6 + x^4 + x^2+ x + 1) 异或 (x^7 + x + 1) =(x^7 + x^6 + x^4 + x^2)
二进制异或:
0101 0111
1000 0011
1101 0100
- 转成16进制
(1101 0100)
2= {D4}乘法计算步骤:
例子:{57} * {83} = {C1}
- 转化
0x57 的二进制: (0101 0111)
2多项式: (x^6 + x^4 + x^2+ x + 1)
0x83 的二进制: (1000 0011)
2多项式: (x^7 + x + 1)
- 相乘
(x^6 + x^4 + x^2 + x + 1) * (x^7 + x + 1) = (x^13 + x^11 + x^9 + x^8 + x^7) 异或 (x^7 + x^5 + x^3 + x^2 + x) 异或 (x^6 + x^4 + x^2 + x + 1) = (x^13 + x^11 + x^9 + x^8 + x^6 + x^5 + x^4 + x^3 + 1)
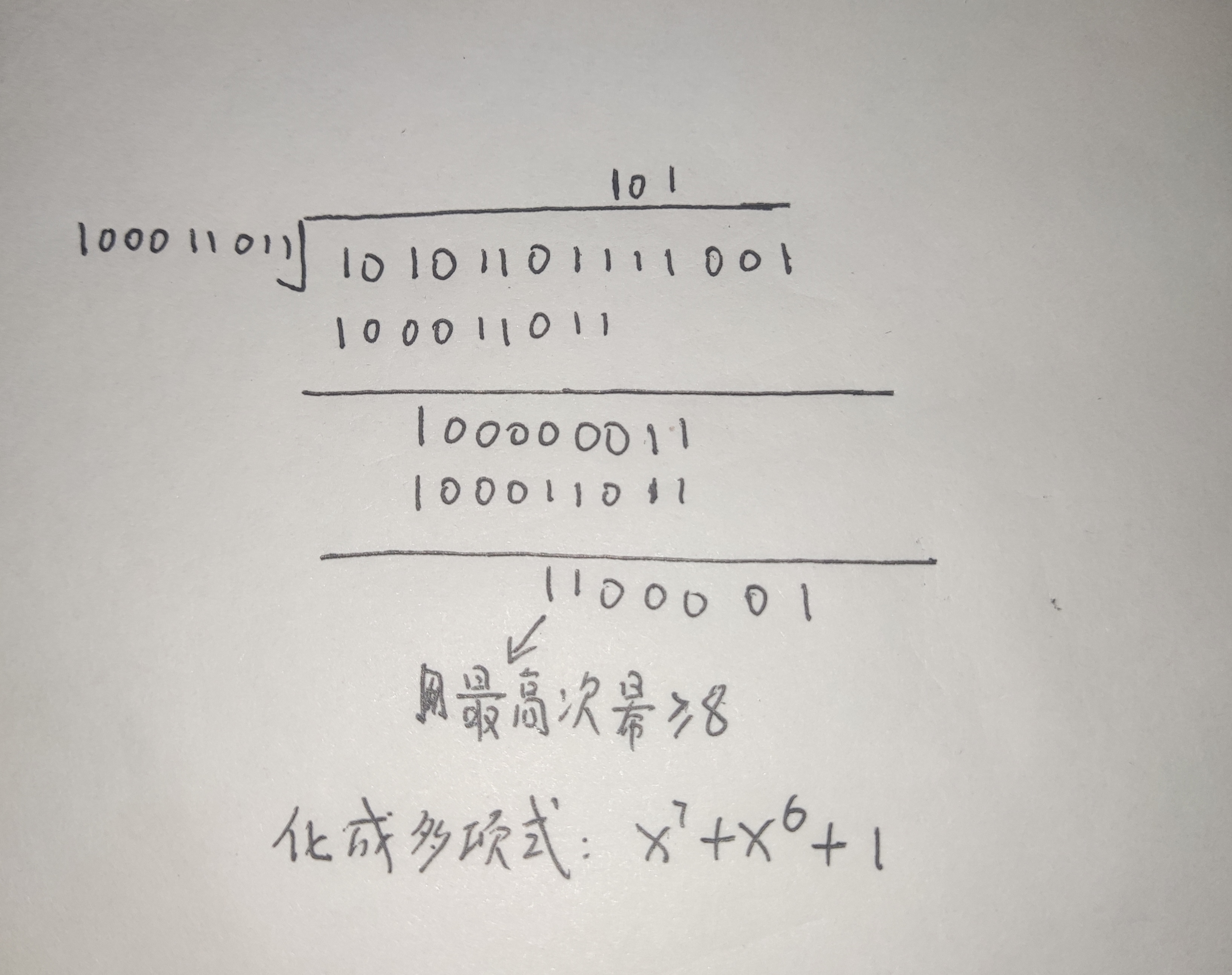
多项式最高次幂≥8需要进行模不可约多项式运算
(x^13 + x^11 + x^9 + x^8 + x^6 + x^5 + x^4 + x^3 + 1) mod ( x^8 + x^4 + x^3 + x + 1) = x^7 + x^6 + 1将多项式转化成二进制进行除法运算得出余数为所求结果
(x^13 + x^11 + x^9 + x^8 + x^6 + x^5 + x^4 + x^3 + 1) = (10101101111001)
2( x^8 + x^4 + x^3 + x + 1) = (100011011)
2
修正:是最高次幂>8
分组密码的工作模式
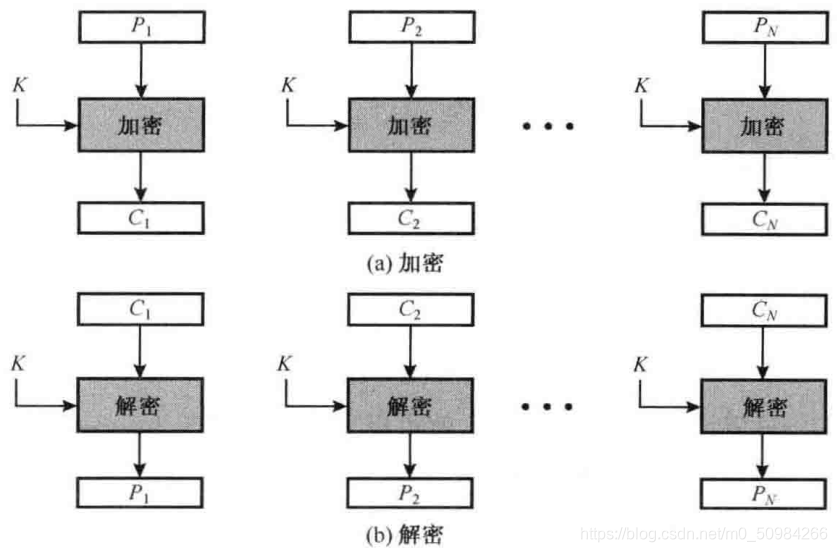
(1)电子密码本模式(ECB)
使用相同的密钥对每个明文分组进行加密,必要时会对最后一个明文分组进行填充。
加密:Ci = Ek(Pi)
直接使用密钥k对当前明文组进行加密就可以得到当前密文组
解密:Pi = Dk(Ci)
直接使用密钥k对当前密文组进行解密就可以得到当前明文组
优点:
- 简单,利于并行计算
- 解密误差不会被传递
缺点:
- 无法隐藏明文的固定格式
- 可能存在对明文分组的攻击
- 传输丢失比特会影响正确解密
(2)密文分组链接模式(CBC)
CBC模式下加密算法的输入是当前的明文组和上一个密文组的异或,进行加密后,输出为当前密文组。
加密:C0 = IV
Ci = Ek(Pi 异或 Ci-1)
每个明文组和上一个密文组进行异或后再加密,就可以得到当前密文组
加密:C0 = IV
Mi = Dk(Ci) 异或 Ci-1
每个密文组分别进行解密,再与上一个密文组进行异或就可以得到当前明文组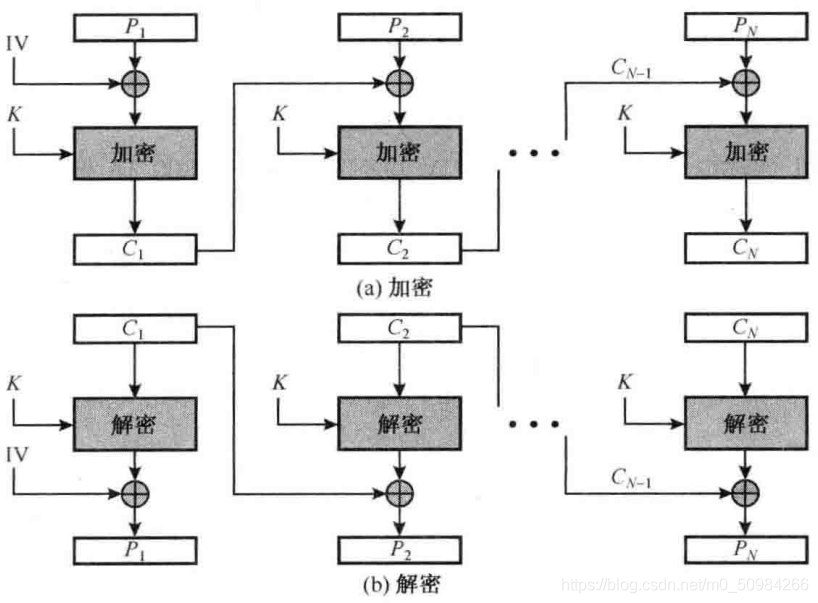
优点:
- 解决的ECB的缺点
缺点:
- 解密误差会被传递,一个明文解密错误会影响下一个明文解密
- 不利于并行运算
- 需要初始化向量IV,并对IV进行严格控制
注意:
- 加密过程中无法对中间的明文进行加密,需要知道前面的明文和IV
- 解密过程中单个密文组损坏(不是长度损坏那种)只会影响当前明文和下一个明文的解密。【密文组已经是正确得出了的,后续可能因为某部分原因导致单个密文组损坏,但是其他密文组是好的,所以才影响两个明文组解密】
(3)密文反馈模式(CFB)
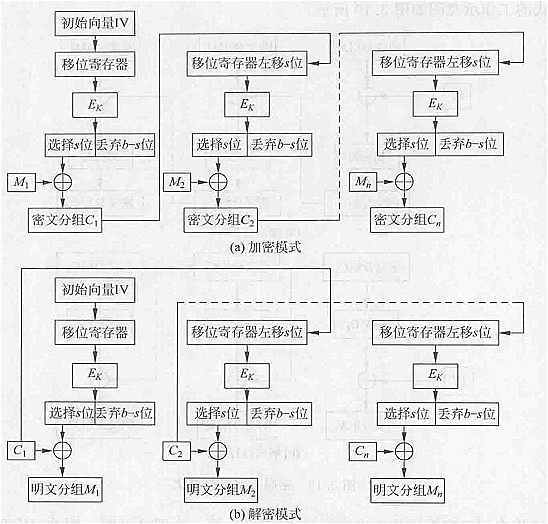
CFB是流密码,特征是明文本身并没有进入加密算法中进行加密,而是与加密函数的输出选择进行异或,得到了密文。
CFB模式下,加密算法的分组长度(假设为b位,即移位寄存器,初始为IV)不会影响明文的分组长度(假设为s位),明文的分组长度s一般是任意的(明文长度必须是s的倍数),如果s=1则一位一位地加密,如果s=8则八位八位地加密。
加密解密内容:
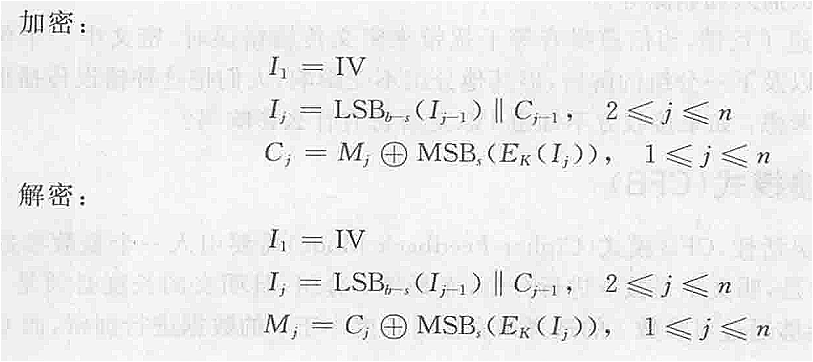
加密函数:输入b位的移位寄存器,值为初始化向量IV
加密函数输出最左边的s位与明文的第一个分段P
1异或得到密文的第一个单元C1,然后将密文发送出去接着移位寄存器左移s位,C1填入移位寄存器的最右边s位。解密的时候,将收到的密文单元与加密函数的输出异或得到明文单元。
其中LSB函数的作用是取低b-s位,MSB函数的作用是取高S位
如LSB
3(111011011) = 011,MSB4(111011011) = 1110
优点:
- 隐藏了明文模式,加密后难以发现固定模式
- 分组密码转化为流密码,明文不参与加密函数
- 可以选择明文长度进行加密,更加灵活
缺点:
- 不利于并行计算
- 解密误差会被传递
- 解密出错影响[b/s]个分组
- 加密出错影响b+1个分组
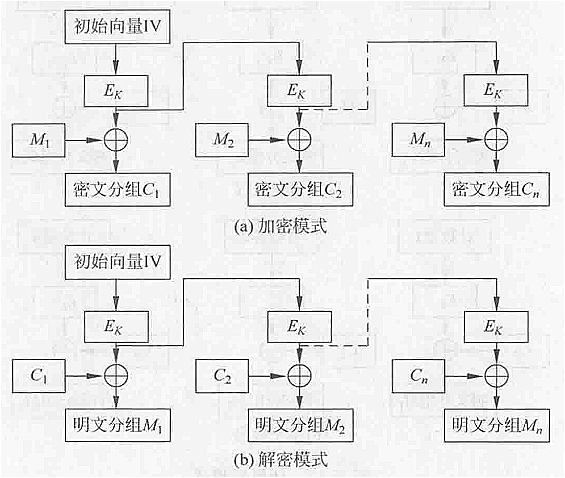
(4)输出反馈模式(OFB)
输出反馈模式通过反复加密初始向量IV来得到密钥流Zk
密钥流:Zk = Ek(Zk-1) [1≤k≤n]
加密:Ci = Pi 异或 Zi
当前密文等于当前明文异或当前密钥Zi
解密:Pi = Ci 异或 Zi
当前明文等于当前密文异或当前密钥Zi
优点:
- 可以并行计算
- 可以加密任意长度的明文(每次加密使用不同的IV)
缺点:
- 对明文的主动攻击是可能的
- IV加密存在误差传送